青橙技术栈 BlogArchivesTagsCategories
卷积神经网络
字数总计: 1.8k|阅读时长: 8 分钟

卷积神经网络中nn.Conv2d()和nn.MaxPool2d()

卷积神经网络之Pythorch实现：

nn.Conv2d()就是PyTorch中的卷积模块

参数列表

参数 作用
in_channels 输入数据体的深度
out_channels 输出数 据体的深度
kernel_size 滤波器（卷积核）的大小 注1
stride 滑动的步长
padding 零填充的圈数 注2
bias 是否启用偏置，默认是True，代表启用
groups 输出数据体深度上和输入数 据体深度上的联系 注3
dilation 卷积对于输入数据体的空间间隔 注4

注：1. 可以使用一 个数字来表示高和宽相同的卷积核，比如 kernel_size=3，也可以使用 不同的数字来表示高和宽不同的卷积核，比如 kernel_size=(3, 2)；

  1. padding=0表示四周不进行零填充，而 padding=1表示四周进行1个像素点的零填充；

  2. groups表示输出数据体深度上和输入数 据体深度上的联系，默认 groups=1，也就是所有的输出和输入都是相 关联的，如果 groups=2，这表示输入的深度被分割成两份，输出的深 度也被分割成两份，它们之间分别对应起来，所以要求输出和输入都 必须要能被 groups整除。

  3. 默认dilation=1详情见 nn.Conv2d()中dilation参数的作用或者CSDN

nn.MaxPool2d()表示网络中的最大值池化

参数列表：

参数 作用
kernel_size 与上面nn.Conv2d()相同
stride 与上面nn.Conv2d()相同
padding 与上面nn.Conv2d()相同
dilation 与上面nn.Conv2d()相同
return_indices 表示是否返回最大值所处的下标，默认 return_indices=False
ceil_mode 表示使用一些方格代替层结构，默认 ceil_mode=False

注：一般不会去设置return_indices和ceil_mode参数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
import torch.nn as nn


class SimpleCNN(nn.Module):
    def __init__(self):
        super(SimpleCNN, self).__init__()
        layer1 = nn.Sequential()
        # 把一个三通道的照片RGB三个使用32组卷积核卷积，每组三个卷积核，组内卷积后相加得出32组输出
        layer1.add_module('conv1', nn.Conv2d(3, 32, (3, 3), (1, 1), padding=1))
        layer1.add_module('relu1', nn.ReLU(True))
        layer1.add_module('pool1', nn.MaxPool2d(2, 2))
        self.layer1 = layer1

        layer2 = nn.Sequential()
        layer2.add_module('conv2', nn.Conv2d(32, 64, (3, 3), (1, 1), padding=1))
        layer2.add_module('relu2', nn.ReLU(True))
        layer2.add_module('pool2', nn.MaxPool2d(2, 2))
        self.layer2 = layer2

        layer3 = nn.Sequential()
        layer3.add_module('conv3', nn.Conv2d(64, 128, (3, 3), (1, 1), padding=1))
        layer3.add_module('relu3', nn.ReLU(True))
        layer3.add_module('pool3', nn.MaxPool2d(2, 2))
        self.layer3 = layer3

        layer4 = nn.Sequential()
        layer4.add_module('fc1', nn.Linear(2048, 512))
        layer4.add_module('fc_relu1', nn.ReLU(True))
        layer4.add_module('fc2', nn.Linear(512, 64))
        layer4.add_module('fc_relu2', nn.ReLU(True))
        layer4.add_module('f3', nn.Linear(64, 10))
        self.layer4 = layer4

    def forward(self, x):
        conv1 = self.layer1(x)
        conv2 = self.layer2(conv1)
        conv3 = self.layer3(conv2)
        fc_input = conv3.view(conv3.size(0), -1)
        fc_out = self.layer4(fc_input)
        return fc_out

model = SimpleCNN()
print(model)

输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
SimpleCNN(
  (layer1): Sequential(
    (conv1): Conv2d(3, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (relu1): ReLU(inplace=True)
    (pool1): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
  (layer2): Sequential(
    (conv2): Conv2d(32, 64, kernel_size=(3, 3), stride=(1, 1))
    (relu2): ReLU(inplace=True)
    (pool2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
  (layer3): Sequential(
    (conv3): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (relu3): ReLU(inplace=True)
    (pool3): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
  (layer4): Sequential(
    (fc1): Linear(in_features=2048, out_features=512, bias=True)
    (fc_relu1): ReLU(inplace=True)
    (fc2): Linear(in_features=512, out_features=64, bias=True)
    (fc_relu2): ReLU(inplace=True)
    (f3): Linear(in_features=64, out_features=10, bias=True)
  )
)

提取模型的层级结构

提取层级结构可以使用以下几个nn.Model的属性，第一个是children()属性，它会返回下一级模块的迭代器，在上面这个模型中，它会返回在self.layer1，self.layer2，self.layer4上的迭代器而不会返回它们内部的东西；modules()
会返回模型中所有的模块的迭代器，这样它就能访问到最内层，比如self.layer1.conv1这个模块；还有一个与它们相对应的是name_children()属性以及named_modules()，这两个不仅会返回模块的迭代器，还会返回网络层的名字。

提取出model中的前两层

1
nn.Sequential(*list(model.children())[:2])

输出：

1
2
3
4
5
6
7
8
9
10
11
12
Sequential(
  (0): Sequential(
    (conv1): Conv2d(3, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (relu1): ReLU(inplace=True)
    (pool1): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
  (1): Sequential(
    (conv2): Conv2d(32, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (relu2): ReLU(inplace=True)
    (pool2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
)

提取出model中的所有卷积层

1
2
3
4
5
conv_model = nn.Sequential()
for layer in model.named_modules():
    if isinstance(layer[1], nn.Conv2d):
        conv_model.add_module(layer[0].split('.')[1] ,layer[1])
print(conv_model)

输出：

1
2
3
4
5
Sequential(
  (conv1): Conv2d(3, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv2): Conv2d(32, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv3): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
)

提取网络参数并对其初始化

nn.Moudel里面有两个特别重要的关于参数的属性，分别是named_parameters()和parameters()。前者会输出网络层的名字和参数的迭代器，后者会给出一个网络的全部参数的迭代器。

1
2
3
for param in model.named_parameters():
    print(param[0])
    # print(param[1])

输出：

1
2
3
4
5
6
7
8
9
10
11
12
layer1.conv1.weight
layer1.conv1.bias
layer2.conv2.weight
layer2.conv2.bias
layer3.conv3.weight
layer3.conv3.bias
layer4.fc1.weight
layer4.fc1.bias
layer4.fc2.weight
layer4.fc2.bias
layer4.f3.weight
layer4.f3.bias

主流神经网络案例分析

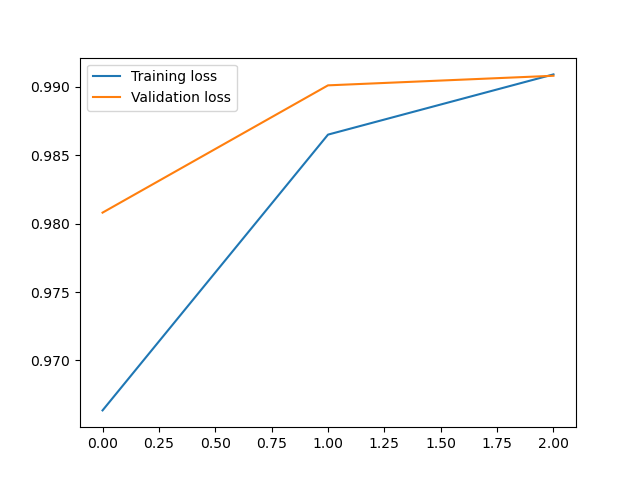
案例：使用卷积神经网络实现对Minist数据集的预测

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
import matplotlib.pyplot as plt
import torch.utils.data
import torchvision.datasets
import os
import torch.nn as nn
from torchvision import transforms


class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        self.layer1 = nn.Sequential(
            nn.Conv2d(1, 16, kernel_size=(3, 3)),
            nn.BatchNorm2d(16),
            nn.ReLU(inplace=True),
        )

        self.layer2 = nn.Sequential(
            nn.Conv2d(16, 32, kernel_size=(3, 3)),
            nn.BatchNorm2d(32),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=2, stride=2),
        )

        self.layer3 = nn.Sequential(
            nn.Conv2d(32, 64, kernel_size=(3, 3)),
            nn.BatchNorm2d(64),
            nn.ReLU(inplace=True)
        )

        self.layer4 = nn.Sequential(
            nn.Conv2d(64, 128, kernel_size=(3, 3)),
            nn.BatchNorm2d(128),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=2, stride=2)
        )

        self.fc = nn.Sequential(
            nn.Linear(128 * 4 * 4, 1024),
            nn.ReLU(inplace=True),
            nn.Linear(1024, 128),
            nn.Linear(128, 10)
        )

    def forward(self, x):
        x = self.layer1(x)
        x = self.layer2(x)
        x = self.layer3(x)
        x = self.layer4(x)
        x = x.view(x.size(0), -1)
        x = self.fc(x)
        return x



os.environ["KMP_DUPLICATE_LIB_OK"] = "TRUE"

data_tf = transforms.Compose(
    [transforms.ToTensor(),
     transforms.Normalize([0.5], [0.5])]
)

train_dataset = torchvision.datasets.MNIST(root='F:/机器学习/pytorch/书/data/mnist', train=True,
                                           transform=data_tf, download=True)

test_dataset = torchvision.datasets.MNIST(root='F:/机器学习/pytorch/书/data/mnist', train=False,
                                          transform=data_tf, download=True)

batch_size = 100
train_loader = torch.utils.data.DataLoader(
    dataset=train_dataset, batch_size=batch_size
)

test_loader = torch.utils.data.DataLoader(
    dataset=test_dataset, batch_size=batch_size
)

model = CNN()
model = model.cuda()
criterion = nn.CrossEntropyLoss()
criterion = criterion.cuda()
optimizer = torch.optim.Adam(model.parameters())

# 节约时间，三次够了
iter_step = 3
loss1 = []
loss2 = []
for step in range(iter_step):
    loss1_count = 0
    loss2_count = 0
    for images, labels in train_loader:
        images = images.cuda()
        labels = labels.cuda()
        images = images.reshape(-1, 1, 28, 28)
        output = model(images)
        pred = output.squeeze()

        optimizer.zero_grad()
        loss = criterion(pred, labels)
        loss.backward()
        optimizer.step()

        _, pred = torch.max(pred, 1)

        loss1_count += int(torch.sum(pred == labels)) / 100
# 测试
    else:
        test_loss = 0
        accuracy = 0
        with torch.no_grad():
            for images, labels in test_loader:
                images = images.cuda()
                labels = labels.cuda()
                pred = model(images.reshape(-1, 1, 28, 28))
                _, pred = torch.max(pred, 1)
                loss2_count += int(torch.sum(pred == labels)) / 100

    loss1.append(loss1_count / len(train_loader))
    loss2.append(loss2_count / len(test_loader))

    print(f'第{step}次训练：训练准确率：{loss1[len(loss1)-1]}，测试准确率：{loss2[len(loss2)-1]}')

plt.plot(loss1, label='Training loss')
plt.plot(loss2, label='Validation loss')
plt.legend()

输出：

1
2
3
4
第0次训练：训练准确率：0.9646166666666718，测试准确率：0.9868999999999996
第1次训练：训练准确率：0.9865833333333389，测试准确率：0.9908999999999998
第2次训练：训练准确率：0.9917000000000039，测试准确率：0.9879999999999994
<matplotlib.legend.Legend at 0x21f03092fd0>

文章作者: Xu Ziao
文章链接: http://www.xuziao.cn/2022/09/23/225609/
版权声明: 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 青橙技术栈！
机器学习