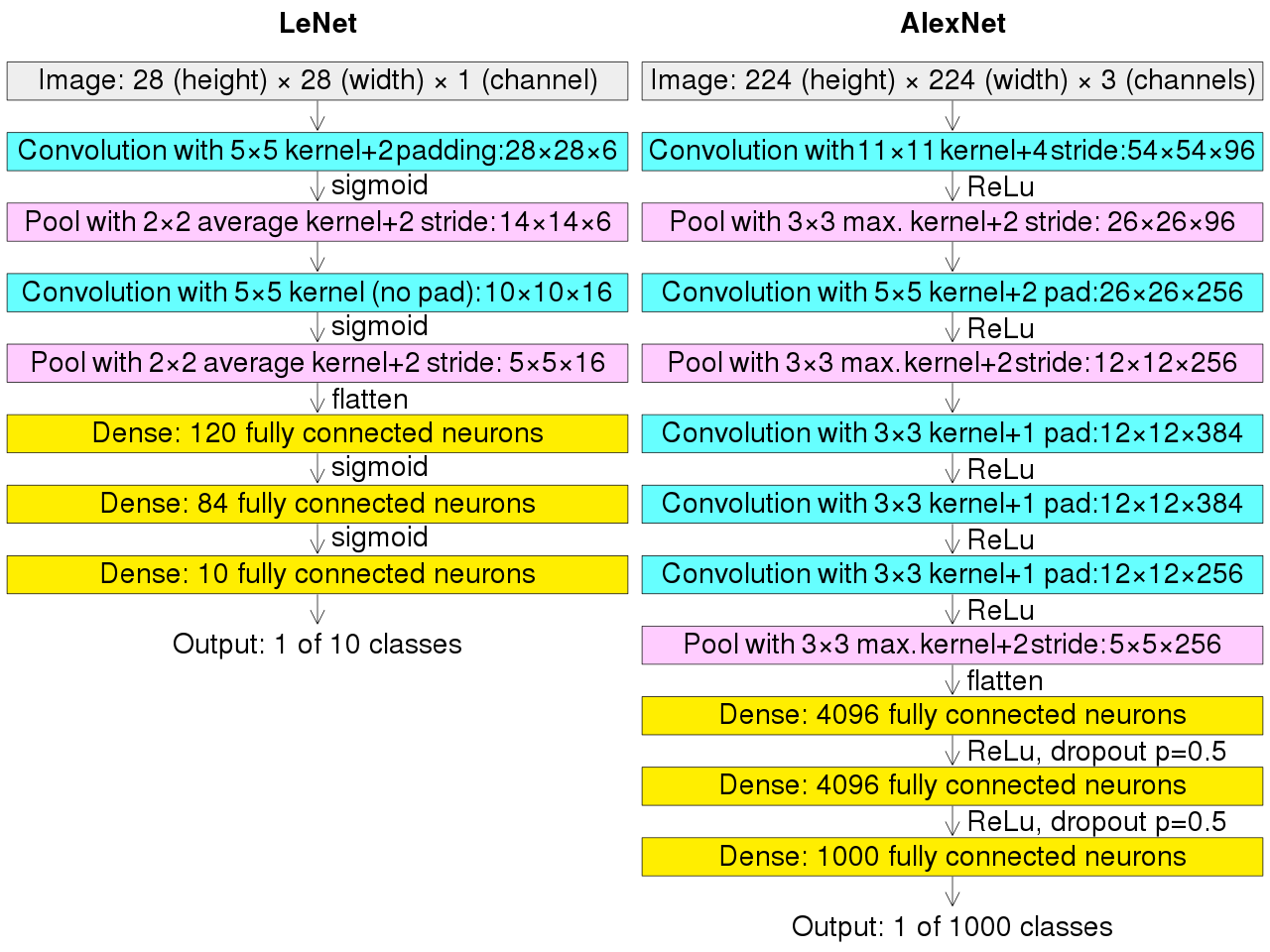
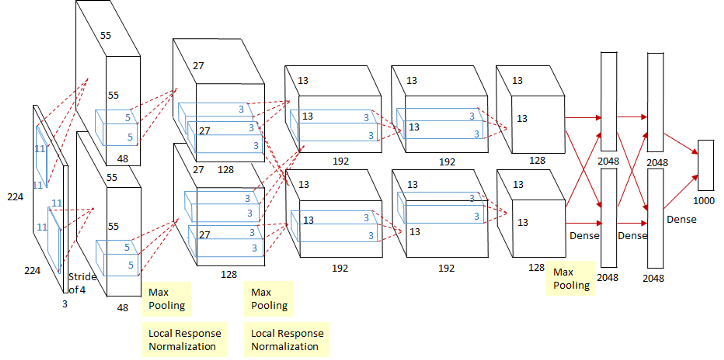
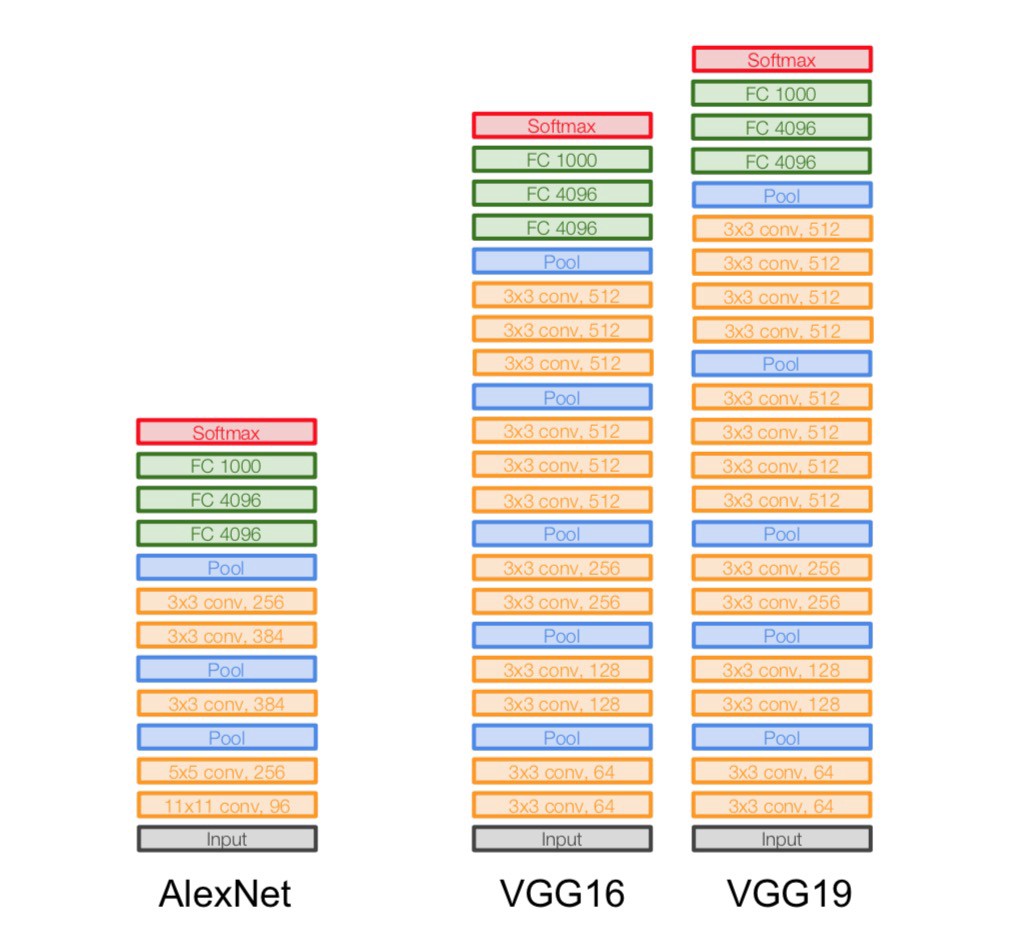
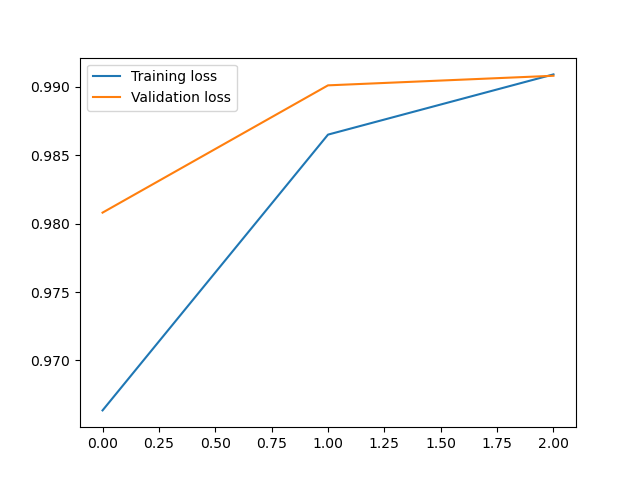
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| import torch.nn as nn
class VGG(nn.Module):
def __init__(self, num_class):
super(VGG, self).__init__()
self.features = nn.Sequential(
nn.Conv2d(3, 64, kernel_size=(3, 3), padding=1),
nn.ReLU(True),
nn.Conv2d(64, 64, kernel_size=(3, 3), padding=1),
nn.ReLU(True),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(64, 128, kernel_size=(3, 3), padding=1),
nn.ReLU(True),
nn.Conv2d(128, 128, kernel_size=(3, 3), padding=1),
nn.ReLU(True),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(128, 256, kernel_size=(3, 3), padding=1),
nn.ReLU(True),
nn.Conv2d(256, 256, kernel_size=(3, 3), padding=1),
nn.ReLU(True),
nn.Conv2d(256, 256, kernel_size=(3, 3), padding=1),
nn.ReLU(True),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(256, 512, kernel_size=(3, 3), padding=1),
nn.ReLU(True),
nn.Conv2d(512, 512, kernel_size=(3, 3), padding=1),
nn.ReLU(True),
nn.Conv2d(512, 512, kernel_size=(3, 3), padding=1),
nn.ReLU(True),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(512, 512, kernel_size=(3, 3), padding=1),
nn.ReLU(True),
nn.Conv2d(512, 512, kernel_size=(3, 3), padding=1),
nn.ReLU(True),
nn.Conv2d(512, 512, kernel_size=(3, 3), padding=1),
nn.ReLU(True),
nn.MaxPool2d(kernel_size=2, stride=2),
)
self.classifier = nn.Sequential(
nn.Linear(512 * 7 * 7, 4096), nn.ReLU(True),
nn.Dropout(),
nn.Linear(4096, 4096), nn.ReLU(True),
nn.Dropout(),
nn.Linear(4096, num_class),
)
self._initialize_weights()
def forward(self, x):
x = self.features(x)
x = x.view(x.size(0), -1)
x = self.classifier(x)
return x
|